hongtlee 님의 블로그
POE - Forward Kinematics 본문
정기구학의 표현법
- D-H parameter을 이용한 표현법
- 지수곱(PoE) 표현법
지수 곱 공식(POE)
스크류축 [S]을 4*4 행렬로 나타내면,

대부분의 6축 로봇은 6R로봇으로, 각 관절이 모든 외부 링크에 스크류 운동을 적용하는 것으로 볼 수 있다.

관절 n이 θn의 변위를 갖는다면, 엔드 이펙터 좌표계 M은 다음과 같다.
$$ T=e^{[S_n]\theta_n}M $$
T∈SE(3)는 엔드 이펙터 좌표계의 새로운 자세이고, Sn = (wn,vn)은 관절 n의 스크류 축을 고정 기반 좌표계로 나타내 것.
마찬가지로 관절 n-1이 변화할 수 있는 상태라면, 이는 링크 n-1에 스크류 운동을 가한 것과 같다.
즉,
$$ T=e^{[S_{n-1}]\theta_{n-1}}(e^{[S_n]\theta_n}M) $$
비슷한 방식으로 모든 관절에 대하여,
$T(\theta)=e^{[S_1]\theta_1}\cdots e^{[S_{n-1}]\theta_{n-1}}e^{[S_n]\theta_n}M$
위 식을 공간 꼴(Space Form)이라 하며, 계산하기 위해서 다음과 같은 조건들이 필요하다.

Example : UR5

엔드이펙터 좌표계{b}는 영 위치에서,

각 링크의 스크류 축 [Si]는 다음과 같다.

θ1 ~ θ6에서 θ2 = -π/2, θ5 = π/2 나머지는 0인 상황일 때,
엔드 이펙터의 자세는,

이때, 길이 단위를 미터로 설정하면

따라서,

Body form 표현
$e^{M^{-1}PM} = M^{-1}e^PM$ 이면 $Me^{M^{-1}PM}=e^PM$ 으로 쓸 수 있다.
지수 곱 공식 Space form의 가장 오른쪽 항부터 n번 반복하면,

이때,
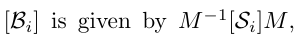

PoE 공식의 space form과 body form의 변환 순서로부터,
공간 꼴에서 M은 가장 멀리 있는 관절에 의해 변환되며, 순차적으로 낮은 번호의 관절에 의해 변환된다. 공간 고정 좌표계에서 표현된 앞 번호 관절의 스크류 축은 뒤 번호 관절 변화에 영향이 없다. 예를 들어, 관절 3의 변화는 관절 2 스크류 축의 공간 좌표계 표현에 영향을 주지 않는다.
마찬가지로, 물체 꼴에서 M은 첫 번째 관절에 의해 변환되며, 순차적으로 뒤 번호의 관절에 의해 변환된다. 공간 고정 좌표계에서 표현된 뒤 번호 관절의 스크류 축은 앞 번호 관절 변화에 영향이 없다. 예를 들어, 관절 2의 변화는 관절 3 스크류 축의 물체 좌표계 표현에 영향을 주지 않는다.
Modern Robotics에서 POE방법으로 Forward kinematics을 푸는 방법과 예제를 보여줬지만, 실제 UR5e에 적용하면 결과가 나오지 않았다.
이유는 스크류 축이 맞게 설정되지 않았기 때문이다.
Appendix C.6을 통해 DH-parameter를 스크류축으로 변환할 수 있다.
(UR robot's DH-parameter)
Universal Robots - DH Parameters for calculations of kinematics and dynamics
Denavit–Hartenberg parameters are used to calculate kinematics and dynamics of UR robots. The definition of the Denavit–Hartenberg parameters can be found here: http://en.wikipedia.org/wiki/Denavit%E2%80%93Hartenberg_parameters Animation to explain th
www.universal-robots.com
Eigen::MatrixXd ComputeSlist(const std::vector<Eigen::Matrix4d>& dh_matrices) {
Eigen::MatrixXd Slist(6, dh_matrices.size());
Eigen::Matrix4d T = Eigen::Matrix4d::Identity();
Eigen::Matrix4d A;
A << 0, -1, 0, 0,
1, 0, 0, 0,
0, 0, 0, 0,
0, 0, 0, 0;
for (size_t i = 0; i < dh_matrices.size(); ++i) {
Eigen::Matrix4d S_skew = T * A * se3Inverse(T);
Eigen::VectorXd S = skew4ToVec6(S_skew);
Slist.col(i) = S;
T *= dh_matrices[i]; // 다음 조인트 위치로 이동
}
return Slist;
}
Eigen::MatrixXd ComputeBlist(const Eigen::MatrixXd& Slist, const Eigen::Matrix4d& M) {
Eigen::MatrixXd Blist(6, Slist.cols());
Eigen::Matrix4d M_inv = se3Inverse(M);
for (size_t i = 0; i < Slist.cols(); ++i) {
Blist.col(i) = skew4ToVec6(M_inv * vec6ToSkew4(Slist.col(i)) * M);
}
return Blist;
}
직접 스크류 축을 구할 수 있다.
1. 회전축 위의 임의의 점 a를 잡고, 원점으로부터 점 a의 위치를 구한다.
2. 회전축 ω의 방향을 구한다.
3. 선속도 $v = a^T \times \omega^T$
이때 회전축 위 임의의 점 a는 회전축으로부터 가장 원점과 가까운 점이라 생각하면 된다.
이제 책의 UR5에 대한 screw list 값과 D-H 파라미터로부터 구한 screw list의 부호가 다름을 볼 수 있는데,
이유는 Base 원점이 z축을 기준으로 180° 회전되어있기 때문이다.
이를 유의하며 스크류축을 구할 필요가 있다.
현재는 Modified DH Paremeter을 고려하지 않고 있으며,
로봇 parameter을 URDF로 표현하는 경우가 잦은데, 언젠가 이로부터 스크류축을 구하려 한다.
Reference
1. Lynch, K. M., & Park, F. C. (2017). Modern robotics. Cambridge University Press.
'Study > Robotics' 카테고리의 다른 글
| 조작성 타원체(Manipulability) (0) | 2025.03.10 |
|---|---|
| Inverse Kinematics (0) | 2025.03.06 |
| Jacobian (0) | 2025.03.06 |
| Lie Theory(2) (1) | 2025.03.05 |
| Lie Theory(1) (0) | 2025.03.04 |




