hongtlee 님의 블로그
Lie Theory(2) 본문
1. 강체 운동
강체의 위치와 방향을 정의하기 위해 숫자 6개가 필요. 이를 체계적으로 서술하기 위해 4*4 행렬을 사용한다.
강체의 속도는 3차원 선속도와 3차원 각속도로 정의되는 R^6 위의 한 점으로 표현할 수 있으며,
이 점을 공간 속도 또는 트위스트라 부름.
→로봇의 상태 공간이 벡터 공간이 아니더라도, 상태 공간의 한 점에서 취할 수 있는 속도의 집합은 벡터 공간을 이룬다.
임의의 강체의 자세는 고정된 기준 좌표계로부터 출발해 일정한 트위스트를 특정 시간동안 적분해 얻을 수 있다.
이런 움직임은 고정된 축을 따라 병진하며, 동시에 그 축을 중심으로 회전하는 스크류 운동과 비슷하다.
→ 모든 강체의 자세를 스크류 운동으로 표현할 수 있으므로(샤를-모치 이론) 지수 좌표(6개의 매개변수로 이루어짐)으로 자세 표현하는 방법이 고안됨
지수좌표의 6개 매개변수는 스크류 축의 방향벡터와 하나의 스칼라 곱으로 이루어져 있으며,
스칼라는 원하는 자세를 나타내기 위해 필요한 스크류 운동의 진행도를 의미함.

(a)가 익히 알고 있는, 회전행렬과 선형이동의 조합으로 강체를 이동시키는 방법이라면,
(b)는 임의의 점을 기준으로 일정 각도만큼 회전시켜 강체를 이동시키는 방법이다.
→(b) 방법을 스크류 운동이라 부르며, 세 개의 스크류 좌표(β, sx, sy)로 표현된다. 만약 선형이동만 존재한다면, 점 s는 무한히 멀리 떨어진 점이다.
→ 더 나아가, 스크류 운동을 선속도 & 각속도를 따라 움직였다고 이해한다면,
점 s를 기준으로 각속도 ω로 회전하고, x방향으로 vx, y방향으로 vy 선속도로 움직인다면,
3차원 벡터 S=(ω, vx, vy)로 표현할 수 있으며 이를 스크류 축 표현이라 한다.(사진에서는 S=(1 rad/s, 2 m/s, 0)이 된다.)
이 스크류 축을 따라 θ = π/2 만큼 회전한다면 원하는 이동이 된다.
→ Sθ = (π/2, π, 0). 이 좌표 표현 방식을 강체 이동의 지수 좌표라 부른다.
⇒ 정리하면, 모든 강체 이동을 고정된 스크류 축에 대해 유한한 회전과 병진으로 나타낼 수 있으며, 이를 강체의 각속도 선속도로 이뤄진 6차원 트위스트를 통해 강체 자세의 6차원 지수 좌표로 표현할 수 있다.
2. Rotations and Angular Velocities
회전행렬의 활용
- 좌표계의 방향을 표현하기 위해
- 벡터나 좌표계를 표현하고 있는 기준 좌표계를 변환하기 위해
- 벡터나 좌표계를 회전하기 위해
회전 행렬 R을 어떤 좌표계의 방향이 아닌 회전 변환으로 간주하는 관점을 부각시키는 표기
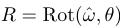
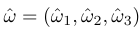
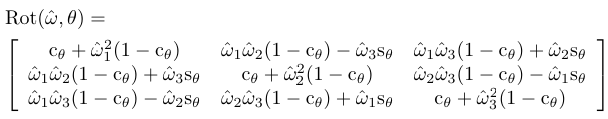
Rsb가 {s}에서 본 어떤 {b}의 방향을 나타낼 때, {b}를 R로 회전하고 싶다고 하자. R은 단위축 ŵ을 중심으로 θ만큼 회전하는 행렬이다.
주의할 점은 단위축 ŵ이 {s}에서 표현한 값인지 {b}에서 표현한 값인지 분명히 해야하는 것이다.
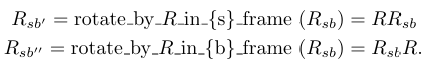
즉, R을 앞에 곱하면 고정좌표계에서 표현한 단위축으로 회전하는 것이고, R을 뒤에 곱하면 물체좌표계에서 표현한 회전축으로 회전시키는 것.
벡터의 경우 벡터를 관여하는 좌표계에서 표현해야 함.
- 각속도
단위축을 갖는 좌표계가 회전하는 물체에 부착되어 있다. 이 단위축의 시간에 대한 미분값을 구하는 것이 목적이다.
물체 좌표계를 시간 t와 t+Δt일때 관측한다면, 좌표계 방향의 변화량은 원점을 지나는 어떤 단위축 ŵ을 중심으로 Δθ만큼 회전한 것으로 표현할 수 있으며 단위축 ŵ은 좌표계에 무관하다.
Δt가 0으로 수렴할 때 ŵ은 그 순간의 회전축으로 볼 수 있다. 한편, ŵ와 dθ/dt로 각속도를 정의할 수 있다.

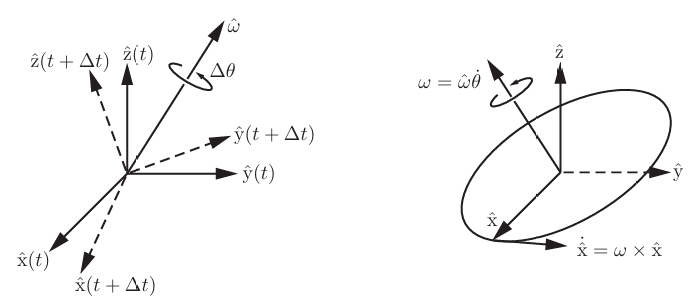
따라서,

마찬가지로 w를 표현할 좌표계를 선택해야 하는데 보통 고정 좌표계{s}와 물체 좌표계{b}를 선택한다.
회전행렬에 대해 각 열은 x,y,z축이므로

[w]은 w의 반대칭행렬 표현이다.
- 회전의 지수 좌표 표현
회전행렬 R의 지수 좌표 ŵθ의 해석
- 초기에 {s}와 일치하던 좌표계가 {s}에서 표현한 축 ŵ를 따라 θ만큼 회전하면 R은 회전한 좌표계의 방향을 {s}에서 표현한 결과가 된다.
- 초기에 {s}와 일치하던 좌표계가 {s}에서 표현한 각속도 ŵθ로 단위 시간만큼 회전하면 (즉, ŵθ를 단위 시간만큼 적분하면) R은 회전한 좌표계의 방향을 {s}에서 표현한 결과가 된다.
- 초기에 {s}와 일치하던 좌표계가 {s}에서 표현한 각속도 ŵ로 시간 θ만큼 회전하면 (즉, ŵθ를 θ만큼 적분하면) R은 회전한 좌표계의 방향을 {s}에서 표현한 결과가 된다.
- 벡터 선형미분방정식

방정식을 풀면,

행렬 지수(matrix exponential)를 테일러 급수 전개하면,

임의의 정방 행렬 A와 스칼라 t에 대해 다음이 항상 성립한다.

따라서,

어떤 n*n 정방 행렬 D와 n*n 가역 행렬 P를 이용해 A = PDP-1로 표현할 수 있다면,

만약 D가 대각행렬이라면,

으로 표현할 수 있다.
- 회전의 지수좌표

p(t)를 이 벡터 끝이 움짐인 경로라고 하면, p(t)의 속도는 dp/dt이다.

이는 선형미분방정식이므로, 해는 다음과 같으며, t와 θ를 치환하면
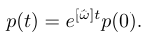
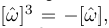
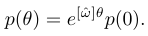
이므로,

따라서,

→ Rodrigues formula
- 회전 행렬의 행렬 로그
만약 ŵθ가 회전행렬 R의 지수 좌표면, 반대칭행렬 [ ŵθ] = [ŵ]θ는 R의 행렬 로그(matrix logarithm) 다.
행렬지수가 각속도 [ŵ]θ를 1초 동안 적분해서 R을 구하듯이, 행렬로그는 R을 미분해서 I를 R로 회전하기 위해 1초 동안 적분해야 하는 특정 각속도 [ŵ]θ를 찾는다.

exp([ŵ]θ)을 전개하면,

전치행렬을 빼면,

sinθ가 0이 아니라면,
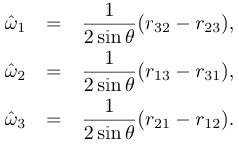
정리하면,

회전행렬 R의 대각합(trace)을 계산하면,

구한 ŵ와 θ을 통해 R을 구할 수 있다.
sinθ가 0인 경우
- kπ, k가 짝수
ŵ와 무관하게 R = I가 되어 ŵ가 정의되지 않음
- kπ, k가 홀수
tr R이 -1이 되며,



- Algorithm
주어진 R ∈ SO(3)에 대해서 exp([ŵ]θ) = R을 만족하는 θ ∈[0, π ]와 단위 회전축 ŵ ∈ R^3, ŵ.norm() = 1을 구한다. → ŵ, θ
벡터 ŵθ ∈ R^3은 R의 지수 좌표이고, 반대칭행렬 [ŵ]θ ∈ so(3)은 R의 행렬 로그이다.
(a) R = I라면, θ = 0 이고, ŵ는 정의되지 않음.
(b) trace R = -1이라면, θ = π다.
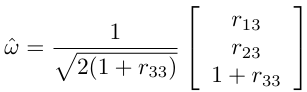
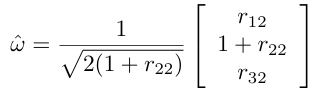
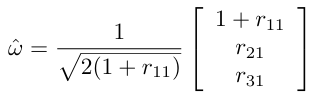
ŵ은 위 셋 중 하나 이며, ŵ가 해일 경우 -ŵ 역시 해이다.
(c)

이면,

⇒ 모든 R은 행렬 로그 [ŵ]θ가 존재하고, 따라서 지수 좌표 ŵθ가 존재한다.
행렬 로그가 계산하는 지수 좌표 w = ŵθ는 ||ŵθ|| ≤ π 를 만족하기 때문에,
R ∈ SO(3)를 반지름 π의 꽉 찬 구로 표현할 수 있다.
모든 회전 행렬 R ∈ SO(3)은 다음과 같은 점 r로 표현할 수 있음.
r = ŵθ
r의 크기는 ||r|| = θ이고 회전 각도를 의미
r의 방향은 ŵ으로, 회전 축의 방향을 의미
구 내부의 점 r ∈ R^3에 대해, ŵ = r/||r|| 을 원점에서 r로 향하는 방향의 단위 벡터로 두고 θ = ||r||을 원점과 r 사이의 거리로 두면
r = ŵθ이 된다. 그러면 r을 ŵ를 중심으로 θ만큼 회전하는 행렬로 볼 수 있다.
⇒ 즉, SO(3)의 모든 회전은 구 내부의 점으로 표현할 수 있음

한편, trace R ≠ -1 인 임의의 R ∈ SO(3)에 대해 exp([r]) = R을 만족하는 유일한 r이 구 내부에 존재한다.
trace R = -1 인 경우, log R에 해당하는 점은 구면에 서로 반대편에 존재하는 두 점으로 주어진다
즉, exp([ŵ]π)=R 와 exp(-[ŵ]π)=R 모두 성립함.
3. Rigid-Body Motions and Twists
- 동차 변환행렬(Homogeneous Transformation Matrices, HTM)
동차 변환행렬 T는 회전 행렬R과 유사.
스크류축 ↔ 회전축
트위스트 ↔ 각속도
강체 운동의 지수 좌표() ↔ 회전의 지수 좌표

성질)

변환 행렬의 곱 = 변환행렬
변환 행렬의 곱셈은 결합 법칙을 만족하며 교환법칙은 성립하지 않음

일때, 벡터 (xT,1)T를 동차 좌표(homogeneous coordinates)라 표현하며, Tx를 Rx + p를 의미하기도 함

변환 행렬의 활용
- 강체의 자세(위치와 방향)를 나타내기 위해
- 벡터나 좌표계를 표현한 기준 좌표계를 바꾸기 위해
- 벡터나 좌표계를 이동시키기 위해
- 스크류 축
스크류 축은 3D 공간에서
물체의 운동(변환)을 나타내는 하나의 축으로, 병진과 회전을 기술
함. 이는 로봇 운동학 및 리 대수에서 SE(3) 군의 기저가 되는 주요 개념
6차원 벡터로 표현된다.

회전 중심: 회전 축 w에 병진 성분 v가 더해져 강체운동을 나타냄.
파라미터화 : 스크류축은 하나의 스크류축과 이를 따라 움직이는 θ 및 거리 d로 운동을 정의할 수 있음.

- 트위스트
트위스트는 강체의 속도운동(선형 속도와 각속도)을 나타내는 6차원 벡터
로, SE(3) 변환의 리 대수 se(3)에서 파생됨
트위스트는 스크류 축과 매우 밀접하게 연결됨.
T를 시간에 따라 변화하는 함수로 보면 움직이는 좌표계의 선속도와 각속도를 고려할 수 있다.

앞서 SO(3)의 회전행렬에 대해 시간에 대한 미분 행렬 \dot R에 앞 또는 뒤에 R^-1을 곱하면 각속도 벡터의 반대칭 행렬이 되는 것을 볼 수 있었다.
마찬가지로 T를 미분한 행렬에 T.Transpose()을 곱하면,


이를 트위스트라 하며, ω와υ을 묶어 6차원 벡터로 타당하다. 또한 SE(3)의 리 대수(se(3))가 된다.

[ω] ∈ so(3)가 되며, υ ∈ R^3 이 된다.
반대로 T.Transpose()을 곱하면, space(공간)에 대한 표기가 되며,

space와 body를 convert해주는 역할이 adjoint matrix(수반 표현)가 된다.
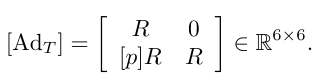
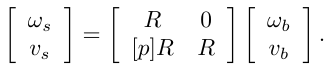
- 트위스트의 스크류 해석
각속도를 회전축과 각속력을 이용해 표현할 수 있듯이 트위스트또한 스크류 축과 스크류 축에 대한 속력을 이용해 해석할 수 있다.
스크류 축 S에 대한 표현을 다음과 같이 하자.
q는 축 위의 임의의 한 점, s_hat은 축 방향을 나타내는 단위 벡터를, h는 스크류 피치를 나타낸다.
스크류 피치 = 선속력 / 각속력

즉,

임의의 점 q를 -sθ x q항이 v에서 스크류축과 수직이 되도록 설정한다면,
항상 임의의 트위스트에 해당하는 {q, s, h}와 속력 θ dot이 존재함을 알 수 있다.
하지만 스크류축 S를 {q, s, h}으로 표기하는 것은 번거롭기 때문에(h가 임의의 값이기 때문),
주어진 스크류 운동에 해당하는 트위스트 V = (w, v) 을 정규화하고 이 값을 이용해 스크류 축을 정의한다.
정규화하면,

6차원 벡터인 스크류축을 4*4 행렬표현[S]로 나타내면 다음과 같다.

- 강체 운동의 지수 좌표 표현
앞서 회전운동의 지수좌표, 행렬로그 표현을 학습함.
결론적으로, 모든 강체 이동은 공간상에 고정된 스크류 축 S에 대한 이동으로 표현할 수 있다.
Homogeneous Transformation Matrices, HTM을 6차원 지수 좌표로 변환.
S는 스크류 축, θ는 identity matrix I에서 T로 만들기 위해 스크류 축을 따라 이동해야 하는 변위량을 의미함.
스크류 축 S의 피치가 유한하면, ||ω|| = 1 이며 θ는 스크류 축에 대한 회전각이 되며
스크류 축 S의 피치가 무한하면, ω = 0, ||v|| = 1 이며 θ는 스크류 축을 따라 이동한 선형 이동이 된다.
회전의 경우와 유사하게 행렬지수와 행렬 로그를 정의하면,

- 행렬 지수
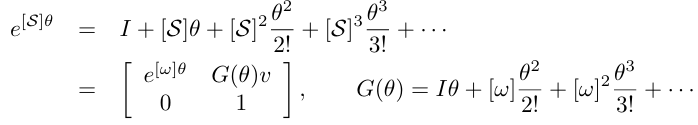
여기서,
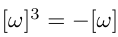
이므로,
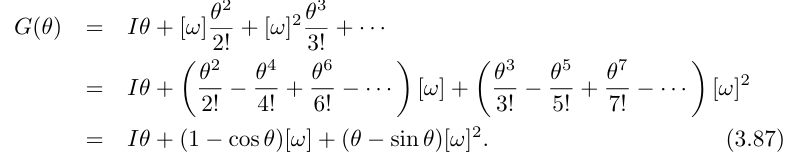
스크류 축 S = (w, v)가 주어질 때,
- ||ω|| = 1

- ω = 0, ||v|| = 1

- 행렬 로그
일반화 시켜서, 임의의 (R, p) ∈ SE(3)에 대해 다음을 만족하는 스크류 축 S = (w, v)과 스칼라 θ가 항상 존재한다.
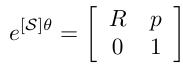
즉, T = (R,p)의 행렬 로그는
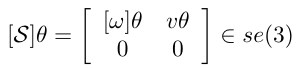
이때 v는 다음과 같다.
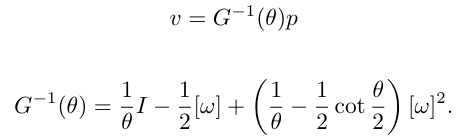
이라 책에 나왔지만, 실제로 실행해보면 값이 올바르지 않다.
이렇게 해서 p와 곱했을 때 se(3)을 구할 수 있었다.
요약하자면, 3차원에서 물체의 이동은 HTM을 통해 나타낼 수 있는데,
이 행렬으로부터 지수 매핑과 로그 매핑을 통해 Lie group과 Lie algebra을 구하는 것이 포스팅의 목표다.
순서대로 HTM의 회전 행렬부분에 해당하는 SO(3)에 대해 먼저 Lie group과 Lie algebra을 구하는 방법을 살펴 봤고,
이어서 SE(3)에 대해 Lie group과 Lie algebra을 구하는 방법에 대해 공부한 것이다.
이렇게 구한 Lie group, Lie algebra 관계를 활용하여 정기구학(POE 방법), 자코비안과 역기구학을 구할 수 있게 된다.
다음 Robotics 포스팅은 정기구학에 대해 소개하겠다.
Lie theory을 이용한 강체의 회전 표현을 C++로 구현함.
포스팅의 내용 및 코드는 Modern Robotics을 참고하여 작성됨.
https://github.com/HongtaeLee-97/RoboticsHong.git
Reference
1. Lynch, K. M., & Park, F. C. (2017). Modern robotics. Cambridge University Press.
'Study > Robotics' 카테고리의 다른 글
| 조작성 타원체(Manipulability) (0) | 2025.03.10 |
|---|---|
| Inverse Kinematics (0) | 2025.03.06 |
| Jacobian (0) | 2025.03.06 |
| POE - Forward Kinematics (1) | 2025.03.06 |
| Lie Theory(1) (0) | 2025.03.04 |




