hongtlee 님의 블로그
Inverse Kinematics 본문
Inverse Kinematics 종류
- 기하학적 기법
- 로봇의 기하학적 구조를 기반으로 삼각함수나 행렬 연산을 통해 해석적 해를 구함.
- 특정 로봇 구조에서만 가능
- 수학적 분석으로 정확한 해를 갖고 매우 빠른 방법
- 구조가 단순한 로봇에 사용됨
- 수치-해석적 기법
- 반복적 계산으로 수렴하며 초가값을 기반으로 근사값 계산
- 대부분의 로봇에 적용가능
- 초기값이 적절하면 빠르게 수렴
- 비선형 방정식 풀이에 적합하며 높은 정확도를 보임
- 역자코비안 풀기
- 최적화 기반 방법(Optimization-Based Approach)
- 휴리스틱 기법
- 경험적 규칙과 데이터를 기반으로 복잡한 환경에서 작동
- 다중 해를 자연스럽게 탐색하며 특이점 문제를 효과적으로 회피.
휴리스틱 기법이 자코비안을 사용한 수치해석적 기법에 비해 빠르다.
Process
Newton - Raphson method
1. 초기 Joint list에 해당하는 Forward Kinematics 구하기
-
- 0 위치일 때 스크류축 :
- 관절 변수 :
스크류 축
where,
스크류 축을 중심으로
where,
(로드리게스 공식)
각 스크류축 및 관절 변수에 대해 지수곱 표현으로 Homogeneous Transformation Matrix을 구한 후 곱해주면, 관절 1 부터 관절 6까지에 해당하는
여기에 0위치에 해당하는 엔드이펙터 자세를 곱해주면, 관절 변수(
---
2. Target matrix와 초기 matrix의 차이에 해당하는 matrix (
---
3.
Using 로드리게스 공식, 회전 행렬 R로 부터
-
- 회전행렬
-
-
-
이 행렬의 성질을 이용하여
한편,
이므로,
따라서,
이렇게
---
4. 트위스트 값으로부터 반복 조건 확인
충분히 작은 에러값
이면 반복.
---
5. 자코비안의 유사역행렬을 이용해 다음 Joint list 구하기
주어진 관절 속도에 대해 트위스트는 다음과 같이 주어진다.
즉,
자코비안의 역행렬은 항상 존재하지 않을 수 있으므로, 유사역행렬(pseudoinverse)
단위시간에 대해
따라서,
---
6. 새로운 Joint list로 과정 1 ~ 5 반복
까지 반복한다.
이때, 얻은
Newton-Raphson방식으로 다음 해를 찾아서, 초기 위치가 굉장히 중요하다. 만약 초기위치가 좋지 않다면 해를 구하지 못하는 경우가 발생한다.
초기위치에 덜 민감하게 invese kinematics을 구하고자 한다면, Runge-Kutta algorithm을 사용하는 것이 좋다.
// Runge-Kutta 4차 알고리듬
auto F = [&](const Eigen::Matrix<double, 6, 1>& theta) {
Tsb_temp = FK_Body(M, Blist, theta);
Tbs_temp = se3Inverse(Tsb_temp);
Tbd_temp = Tbs_temp * targetMat;
twist_b_skew_temp = SE3Tose3(Tbd_temp);
twist_b_temp = se3ToVec6(twist_b_skew_temp);
Jb = Jacobian_Body(Blist, theta);
Jb_pseudoinv = computeJacobianInverse(Jb);
return Jb_pseudoinv * twist_b;
};
...
k1 = F(eigentheta);
k2 = F(eigentheta + 0.5 * dt * k1);
k3 = F(eigentheta + 0.5 * dt * k2);
k4 = F(eigentheta + dt * k3);
eigentheta += (dt / 6.0) * (k1 + 2.0 * k2 + 2.0 * k3 + k4);
...
대신 Newton-Raphson방식보다 시간이 오래 걸린다. 또한 휴리스틱 역기구학 기법인 Fabrik 등에 비하면 굉장히 느리다.
자코비안을 통해 역기구학 해를 얻은 경우, 하나의 해를 구할 수 있는데,
해의 분기에 따라 역기구학 해는 16개의 해를 가질 수 있다.
모든 해를 구하는 알고리즘에 대해서 공부하고 있다.
Redundant Manipulators
Joint가 7개인데 6축 로봇이라던가 자유도가 남는 로봇이 있다면, Null space을 활용할 수 있어진다.
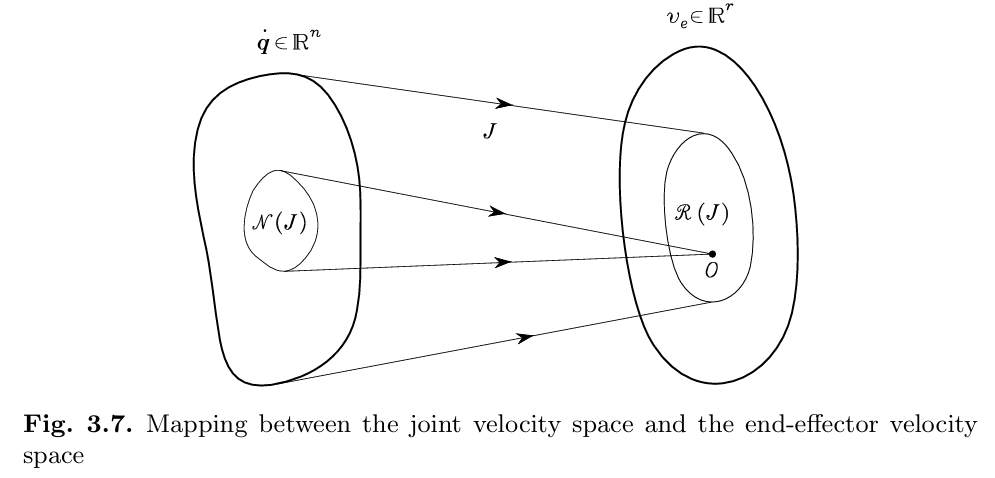
비용함수로써 초기 위치와 가장 근접한 해를 선택하도록 추가 항(
자유도가 남으므로,
// Convenient utilization of redundant DOFs 계산
auto computeSecondaryObjectiveGradient = [&](const Eigen::Matrix<double, 6, 1>& q) -> Eigen::Matrix<double, 6, 1> {
// Manipulability gradient
Eigen::MatrixXd Jb = Jacobian_Body(Blist, q);
Eigen::MatrixXd JJT = Jb * Jb.transpose();
// Gradient of manipulability measure
double manipulability = std::sqrt(JJT.determinant());
Eigen::Matrix<double, 6, 1> grad;
grad.setZero();
for (int i = 0; i < q.size(); ++i) {
// Numerical gradient computation
Eigen::Matrix<double, 6, 1> q_perturbed = q;
double epsilon = 1e-6;
q_perturbed[i] += epsilon;
Eigen::MatrixXd Jb_perturbed = Jacobian_Body(Blist, q_perturbed);
double manipulability_perturbed = std::sqrt((Jb_perturbed * Jb_perturbed.transpose()).determinant());
grad[i] = (manipulability_perturbed - manipulability) / epsilon;
}
return grad;
}
// Secondary objective: joint limit 중심 유지
Eigen::Matrix<double, 6, 1> q_dot_0 = k0 * computeSecondaryObjectiveGradient(eigentheta);
// Null-space projection
delta_theta = Jb_pseudoinv * twist_b + (Eigen::Matrix<double, 6, 6>::Identity() - Jb_pseudoinv * Jb) * q_dot_0;
이런 식으로 구현해주면 된다.
Reference
1. Lynch, K. M., & Park, F. C. (2017). Modern robotics. Cambridge University Press.
2. Sciavicco, L., Villani, L., SICILIANO, B., & ORIOLO, G. (2010). Robotics: modelling, planning and control. Springer.
3. https://ropiens.tistory.com/198
'Study > Robotics' 카테고리의 다른 글
| MoveL Test (check possibility) (0) | 2025.03.11 |
|---|---|
| 조작성 타원체(Manipulability) (0) | 2025.03.10 |
| Jacobian (0) | 2025.03.06 |
| POE - Forward Kinematics (1) | 2025.03.06 |
| Lie Theory(2) (1) | 2025.03.05 |




