Arc Sensing
로봇 용접에 용접선 추출 후 용접을 시작하더라도,
추출한 용접선 자체에 노이즈나 에러가 있거나, 용접환경에 의해 실제 용접 궤적이 뒤틀릴 수 있다.
용접 궤적을 실시간으로 바로 잡을 필요가 있는데, 다양한 방법이 존재한다.
그 중 하나인 아크센싱을 적용하고자 한 자료조사 내용이다.
스스로 공부한 내용이라 틀린내용 지적 환영입니다.
이론적 배경
- 금속결합은 금속 원자들이 자유롭게 움직이는 전자(자유전자)를 공유하며 형성되는 결합. 금속 내부에서 원자들은 격자 구조를 이루고 있으며, 전자들이 자유롭게 이동하면서 전체 금속을 결속하는 역할
- 두 금속을 결합하기 위해서는 표면의 불순물이나 산화막을 제거하여 금속의 순수한 표면을 노출시켜야 함. 이는 결합을 방해하는 요소들을 제거하고 금속 원자들이 가까이 접근할 수 있게 함.
- 용접 시 열을 가하면 금속이 용융되어 액체 상태로 변화. 이때 두 금속의 경계선에서 원자들이 서로 확산하고 혼합되어 한 덩어리로 이어집니다.
- 이후 냉각되면서 액체 상태의 금속이 고체로 재결정되며, 이 과정에서 금속 원자들이 서로 결합하여 하나의 연속적인 격자 구조를 형성.
- 금속 원자의 격자 구조가 형성되며 금속결합이 이뤄지고, 두 금속이 기계적으로, 물리적으로 강하게 결합
따라서 충분히 녹고, 잘 냉각되어야 균일한 금속이 생성되는 것.
금속이 용융되기 위한 열에너지 공급(열입력)
$$ Q=(V⋅I⋅η)/S $$
- Q: 열입력 (J/mm 또는 kJ/mm)
- V: 전압 (V)
- I: 전류 (A)
- η: 용접 효율 (효율 값, 일반적으로 0.6~0.9)
- S: 용접 속도 (mm/s)
즉, 단위길이당 공급된 에너지.
용접 효율은 일반적으로 사용되는 값이 있음.
- MIG/MAG 용접: 0.8~0.9
- TIG 용접: 0.6~0.7
- 플라즈마 용접: 0.6~0.8
- 아크 용접 (SMAW): 0.7~0.8
하지만, 본 실험에서는 정확한 열입력 값이 필요한 것이 아닌, 상대적인 값이 필요하기때문에 용접 효율은 그렇게까지 정확할 필요는 없어보임.
전력에 대한 공식
$$ P = VI = I^2R $$
이고, R은 용접 토치에 튀어나온 와이어로 볼 수 있음.
저항R은 다음과 같이 표현 가능하다. $ R=ρL/A $
즉, 와이어의 길이에 비례하는 저항.
선택의 필요성: 고정 전압을 믿고 Q를 전류에 비례하게 할 지, 전류의 제곱에 비례하게 할 지 정해야 함. 전류의 제곱에 비례한다고 식을 세운다면 저항값을 추정할 근거를 세워야함.
정리하면, 전압, 전류, 와이어 길이로 용접에 사용되는 에너지를 계산할 수 있으며, 이는 용융 정도에 비례하게 됨. 열입력Q를 일정하게 유지시킨다면, 아크 길이와 위치가 어느정도 목표하는 지점에 위치한다고 볼 수 있음
따라서 전류 I가 변화함에 따라 열입력 Q를 어느정도 계산할 수 있으며, 값의 오차에 따라 로봇을 움직여 위치를 보상할 수 있다.
예를 들어, Q가 기준치보다 크다면, 진폭을 줄이거나(tool y -) 용접토치를 후퇴(tool z -)시킬 수 있고, Q가 기준치보다 작다면 진폭을 줄이거나(tool y +) 용접토치를 후퇴(tool z +)시킬 수 있을 것이다.
위치가 똑바르다면 토치 이동 속도를 조절하는 방식으로 Q를 조절할 수 있을 것이다.
다만, 한계가 있다면 input으로 쓰이는 data는 전류값 하나인데, 조절할 수 있는 값은 tool y, tool z, speed가 있다. 또한, 센서로 읽는 값이므로 노이즈가 생겨 이를 보정할 필터 역시 적용해야하는 문제가 있다. 더욱 나아가서는 전류 data를 취득할 방법과 로봇 움직임에서 보상값 적용 방안을 고려해야 한다.
방안 1) 기준치에서 벗어난 오차값의 크기에 따라 전략을 나눔. 예를들어, 오차가 적다면 tool y만 적용, 오차가 크다면 tool y와 tool z 동시 적용하되 7:3 비율로 적용 등
실시간으로 보상값을 적용해 값을 수정해야 하며, 기존 dwell/ndwell 구간을 어떻게 설정하고 Q의 기준치 설정 방법에 대해 논의해야 할 필요가 있다.
용접품질에 영향을 끼치는 매개변수는 다양하지만 로봇이 통제 가능한 용접매개변수는 결국 용접 위치와 용접 속도.
용접 속도(토치 이동 속도) 조절을 통한 아크 센싱 보정도 고려해볼 가치가 있음.
→ 용접 토치가 정확하게 위치했을 조건 하에 고려.
Current - time 그래프를 통한 보정
전류와 tip_to_workpiece 길이에 대한 수학적 모델링
참고 논문)
Kim, J. W., & Na, S. J. (1991). A study on prediction of welding current in gas metal arc welding part 1: modelling of welding current in response to change of tip-to-workpiece distance. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 205(1), 59-63.
고정 전압 시스템, 시간당 전류 변화량과 tip to distance의 관계를 통해 기준치로부터 전류가 벗어난 정도를 측정
와이어가 공급될때, 옴의 법칙에 따라 가열되며 연장 길이에 비례하여 선형적으로 증가함. wire extension 끝 부분의 단위 부피당 열 함량 $ H_e $는 다음과 같다.
$$\mathbf{H}_e = \frac{\lambda_1 L_c j^2}{\omega} - \lambda_2$$,
여기서 $\lambda_1$는 와이어의 **고온 저항률** $[\Omega \cdot \text{mm}]$,
$\lambda_2$는 와이어의 **상온 저항률** $[J \cdot \text{mm}^{-3}]$ 이다.
또한, L은 전극 연장 길이, w는 와이어 공급 속도, j는 용접 전류 밀도이다.
$$\mathbf{V}_e = \frac{\omega}{j} \mathbf{H}_e = \lambda_1 L_e j - \lambda_2 \frac{\omega}{j}$$
steady state에서 와이어 공급속도는 와이어가 녹는 속도와 같음. wire가 녹아 droplet이 될때 부피당 열 함량을 $ H_0 $라 할 때, anode tip에서의 받는 열($ H_a $)은 다음과 같다.
$\mathbf{H}_a = \frac{\phi j}{\omega}$. $\phi$ 는 유효 용융 전위.
$\mathbf{H}_0 = \mathbf{H}_e + \mathbf{H}_a$
이고, $H_e$를 대입하면,
$\omega = \frac{1}{H_0} (\phi j + \omega H_e)$ , $\omega = \frac{1}{H_0 + \lambda_2} (\phi j + \lambda_1 L_e j^2)$
$\phi$와 $H_0$ 는 물질에 따라 결정되며, 전극 연장 길이(L), 와이어 공급 속도( $\omega $), 용접 전류 밀도(j)와는 독립적이다. 마찬가지로 λ1, λ2역시 물질에 따라 값이 결정된다.
- steel : λ1= 1.2 x 10^-3 ohm mm
- Si-Mn steel : λ2= 3.98 J mm^-3
- in this case, $H_0$ = 11.1 J mm^-3, $\phi$ = 3.48V
전류 밀도 j는 전류(I)에 와이어 단면적(A)을 나눈 값. 따라서,
$V_e = \frac{\lambda_1 L_e I}{A} - \frac{\lambda_2 \omega A}{I}$
한편, 아래 식을 $ L_e$ 에 대해 정리하면 다음과 같다.
$\omega = \gamma_1 j + \gamma_2 L_e j^2$, $L_e = \frac{A^2 \omega - \gamma_1 I A}{\gamma_2 I^2}$
tip to workpiece 거리 L은, 와이어 연장 길이(Le)에 아크 길이(L_a)를 합한 것과 같다.
아크 전압(Va), 용접 전류, 아크 길이에 대해 실험적으로 정의된 방정식: Aryton’s equation을 사용하면,
$V_a = \kappa_1 L_a + \kappa_2 + (\kappa_3 L_a + \kappa_4) I$
카파 1 ~ 4의 값은 상수값(실험값)으로 정해지며, 이 논문에서는
$V_a = 0.6315 L_a + 15.22 + (1.02 \times 10^{-5} L_a + 3.07 \times 10^{-2}) I$
일반적으로, gmaw용접 시스템에서 일정 전압을 사용함.
일정 전압 전원 장치를 선택하는 이유는 시스템에 내재된 자체 보정 아크 길이 기능 때문.
일정 전압 시스템은 용접 중 쉽게 발생하는 접촉 팁과 작업물 간의 거리 변화를 보상하여, 원하는 아크 길이를 유지하기 위해 자동으로 증가하거나 감소된 용접 전류를 공급

따라서, (n은 전원 공급 장치의 제원으로 추측됨)
\(\frac{\Delta V}{\Delta I} = -n\)
시간에 대해 미분하면,
\(\frac{dV}{dt} = -n \frac{dI}{dt}\)
이제, $V_e$와 $V_a$를 시간에 대해 미분하고, $L_a = L - L_e$임을 이용해서 식을 정리하면,
$V_e = \frac{\lambda_1 L_e I}{A} - \frac{\lambda_2 \omega A}{I}$, $V_a = \kappa_1 L_a + \kappa_2 + (\kappa_3 L_a + \kappa_4) I$, $L_e = \frac{A^2 \omega - \gamma_1 I A}{\gamma_2 I^2}$
\[
\frac{dI}{dt} =
\frac{-(\kappa_1 + \kappa_3 I) \gamma_2 I^3}
{(\kappa_3 L + \kappa_4 + n) \gamma_2 I^3 - (\kappa_1 + \kappa_3 I)(\gamma_1 I - 2 A \omega) A - (A \omega - \gamma_1 I) \kappa_3 I A + (\gamma_2 \lambda_2 - \lambda_1) A \omega I} \frac{dL}{dt}
\]
시간에 따른 전류와 길이(tip to workpiece) 변화에 대한 미분방정식을 얻게 됨.
위의 방정식을 통해 접촉 팁과 작업물 간 거리의 변화에 따라 전류의 변화를 계산할 수 있다.
용접 전류는 접촉 팁과 작업물 간 거리가 선형적으로 감소하거나 증가하는 경우에 대해 룽게-쿠타 (Runge-Kutta) 방법등의 수치 해석 기법을 사용하여 계산할 수 있다.
논문에 이어진 실험은 위 수학적 모델을 검증하기 위한 실제 실험.
Halmoy(5)는 Ar, CO 및 이 둘의 혼합 기체에 대해서는 Ho와 Φ값이 크게 변하지 않는다고 언급
따라서 식 (5)의 상수들 λ1, λ2, Ho, Φ 중에서, 전극 와이어의 저항률과 관련된 상수인 λ1만이 재료에 의존하는 상수
λ2에 대해서는 Si-Mn steel electrode wire에 대한 λ2 사용
회전 아크센서의 수학적 모델링을 바탕으로 한 심트래킹 및 용접끝점 탐지
Shi, Y. H., Yoo, W. S., & Na, S. J. (2006). Mathematical modelling of rotational arc sensor in GMAW and its applications to seam tracking and endpoint detection. Science and technology of welding and joining, 11(6), 723-730.

접근은 비슷하다. 우선 와이어 전압을 구한다.
$V_e = \frac{a L_e I}{S} - \frac{b v_f S}{I}$, V=IR이므로,
$R_e = \frac{V_e}{I} = \frac{a L_e}{S} - \frac{b v_f S}{I^2}$
melting rate of wire, vm은 다른 논문에서 구했으나, 해당 논문 찾질 못해서 유도 과정은 생략..
$v_m = \frac{A I}{1 - B \left( \frac{L_e}{v_f} \right) I^2}$, $A = \frac{\psi}{S(H_o + b)}$, $B = \frac{a}{S^2(H_o + b)}$
ψ는 실험적으로 얻어지는 값.
앞선 논문의
$\omega = \gamma_1 j + \gamma_2 L_e j^2$ 에서,
γ1, γ2와 A, B는 형태가 비슷하다. 앞 논문에서 steady state로 가정하고 와이어 공급속도를 melting rate와 같다고 가정했는데, 본 논문에서는 따로 구한 듯 함.

$V_s = V_{oc} - R_s I - L_s \frac{dI}{dt}$
$V_p = R_p I + L_p \frac{dI}{dt}$
$V_a = V_{a0} + R_a I + E_a L_a$
$V_{oc}$, $R_s$, $L_s$는 용접 전원기에서 결정됨.
$V_p$, $R_p$, $L_p$는 용접 cable에 대한 영향.
$V_{a0}$는 용접 모델의 상수값(아마 초기값인듯 하다).
$R_a$, $L_a$, $E_a$ : Arc의 저항, 길이, 전기장.
위 식들을 정리해, $\frac{dI}{dt}$, $\frac{dL_e}{dt}$를 구하면,
$\frac{dL_e}{dt} = v_f - v_m = v_f - \frac{A I}{1 - B (L_e / v_f) I^2}$
$\frac{dI}{dt} = \frac{V_{oc} - V_{a0}}{L_s + L_p} - \frac{R_s + R_p + R_a + \frac{a L_e}{S}}{L_s + L_p} I + \frac{b S v_f}{(L_s + L_p)} I - \frac{E_a}{L_s + L_p} L_a$
이 논문에서는 회전 아크센서를 사용. 일종의 위빙을 만들어 주는 센서로 이해했음.

시간에 따른 와이어 위치를 구함
$^{w}P =
\begin{bmatrix}
r \sin(2\pi\omega t) + v_w t \\
r \cos(2\pi\omega t) \cos\phi + l_e \sin\phi + y_0 \\
r \cos(2\pi\omega t) \sin\phi - l_e \cos\phi + z_0
\end{bmatrix}$
아크는 와이어 끝과 수평 작업물 또는 수직 측벽 사이의 최단 경로로 생성된다고 가정
그러면 용접 프로파일을 고려하지 않은 조건에서, 필릿 조인트 용접 시의 아크 길이 La는 벡터 MP의 Y 성분과 Z 성분 중 최소값이어야 하며, 이는 다음과 같이 표현될 수 있음.
$L_a = \min \{ [r \cos(2\pi\omega t) \cos\phi + l_e \sin\phi + y_0], [r \cos(2\pi\omega t) \sin\phi - l_e \cos\phi + z_0] \}$
용접 전류, 와이어 연장 길이, 그리고 아크 길이는 4차 룽게-쿠타 수치 해석 방법을 사용하여 미분 방정식 (7), (8), (16)을 동시에 해결함으로써 동적으로 계산할 수 있음.
(7)
$\frac{dL_e}{dt} = v_f - v_m = v_f - \frac{A I}{1 - B (L_e / v_f) I^2}$
(8)
$\frac{dI}{dt} = \frac{V_{oc} - V_{a0}}{L_s + L_p} - \frac{R_s + R_p + R_a + \frac{a L_e}{S}}{L_s + L_p} I + \frac{b S v_f}{(L_s + L_p)} I - \frac{E_a}{L_s + L_p} L_a$
(16)
$L_a = \min \{ [r \cos(2\pi\omega t) \cos\phi + l_e \sin\phi + y_0], [r \cos(2\pi\omega t) \sin\phi - l_e \cos\phi + z_0] \}$
다음 테이블은 실험에 사용된 상수값 및 매개변수.

아크길이는 사실, 기존 용접 비드에 영향을 받음.
아크가 와이어 끝과 수평 작업물, 수직 측벽, 또는 용접 비드 표면 간의 최단 경로로 생성되는 경우, 필릿 용접 시의 아크 길이는 다음과 같이 주어짐.
La=min(YMP,ZMP,dbead) - - - 벡터MP의 Y 및 Z 성분, 용접 비드 표면까지의 거리
Assumpition)
- 용접된 와이어의 부피는 형성된 용접 비드의 부피와 동일하다.
- 비드의 단면은 삼각형 모양이다.

삼각형 평면, x-y평면, z-x 평면 중 와이어 끝단과 가장 가까운 거리로 아크 발생
→ 아크 길이
$L_a =
\min \Bigg\{
[r \cos(2\pi\omega t) \cos\phi + l_e \sin\phi + y_0],
[r \cos(2\pi\omega t) \sin\phi - l_e \cos\phi + z_0],
\frac{\frac{1}{7} M x_w + \frac{2}{h} M y_w + \frac{2}{v} M z_w - 1}
{\left[ \left(\frac{1}{7} \right)^2 + \left(\frac{2}{h_{\text{bead}}} \right)^2 + \left(\frac{2}{v_{\text{bead}}} \right)^2 \right]^{1/2}}
\Bigg\}$
와이어로부터 시간당 drop되는 와이어의 부피와 용접 비드 부피가 동일하므로,
1/2 * v_bead * h_bead * v_w (weld bead) = π(d/2)^2*v_f (droplet volume)
한편, y-z 평면에서 용접 토치 회전 축과 v_bead, h_bead 직선이 수직하므로 기울기로부터 v_bead/h_bead 관계식 구할 수 있음
$h_{\text{bead}} = \left( \frac{\pi d_w^2 v_f M y_{tc}}{2 v_w M z_{tc}} \right)^{1/2}$
$v_{\text{bead}} = \left( \frac{\pi d_w^2 v_f M z_{tc}}{2 v_w M y_{tc}} \right)^{1/2}$
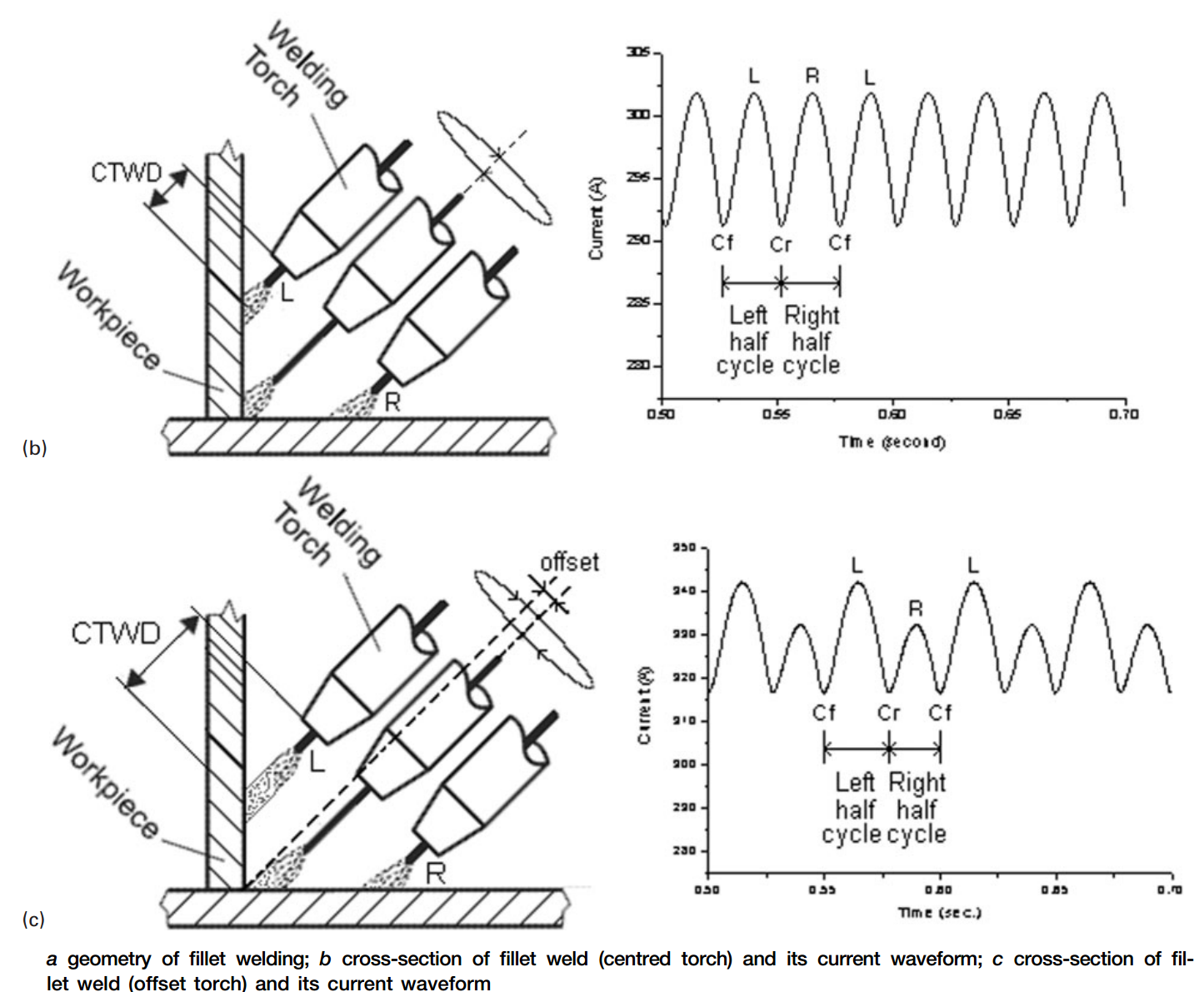
시간에 따른 전류, 아크 길이 그래프를 그릴 수 있게 됨. (시간에 따른 와이어 길이 → 시간에 따른 아크 길이 → 시간에 따른 전류)
- 전류값이 크다 = tip_to_workpiece 가 가깝다 = weave maximum point 반대로, 전류값이 작을 때는 center에 위치
- I - time 그래프에서 극대값 끼리의 차이로 y축 보정 (I(L)값이 I(R)값보다 크면 +y 보정 등)
- I - time 그래프에서 I의 극소값을 통해 z 축 보정 (너무 작아지면 tool을 더 가깝게 보정 등)
따라서, I - time 그래프를 그릴 수 있어야 함.
추가로, Current - time 그래프에서, local maxima - local minima 차이의 크기를 통해 용접심의 끝점을 추정. 값이 갑자기 커진다면 용점심이 끝난 것으로 판단.
다만 이 방법을 사용한다면 용점심이 끝난 것이 직육면체 등의 꼭짓점인 경우 등의 한계가 있을 듯하며, 끝나고도 한 사이클을 더 용접해야 하는 단점이 있어보임.
- 아크센싱 모듈을 통해 직접적으로 전류를 측정함으로써, 이론적 그래프가 아닌 노이즈가 포함된 Current - time를 얻게됨.
- 아마 노이즈 보정을 위해 trapezoidal weave motion을 권장하고 Current - time 그래프의 극대값들만 비교, 극대점의 차이를 통해 y축보정, 값의 크기로 z축 보정하는 것으로 추정됨.
- 전류 변화에 따른 보정값 수치 결정 문제. 만약 수학 모델링 결과를 알고 있다면, 역으로 current차이에 따라 필요한 보정 수치를 계산할 수 있을 것. 모델링을 하지 않으면 경험적으로 보정 수치값을 생성해야 할 듯?
- 만약 다른 weave motion을 한다면, Current - time 그래프를 잘 얻고 노이즈 필터링을 잘 할 필요가 있음.
- 더 나아가서, 각 weaving motion에 따른 수학적 모델링을 통해 이론적 Current - time 그래프를 얻고, 해당 그래프 개형 따라 피팅해서 값을 얻는 방법이 있을듯.
현재 UR5e를 사용하고 있는데, URControl을 통해 스크립트 형태로 명령어를 보냄.
아크센싱과 같은 실시간성 보장을 위해서 RTDE를 사용할 필요가 있어 실제 실험으로 넘어가지 못하고 있음.